Everyone Talks About Insecure Randomness, But Nobody Does Anything About It
In which I take a crack at pointing a neural network at random noise, and achieve 95+% predictive bitwise accuracy against my hated foe in this world, Xorshift128.
John Labelle
"Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin."
What exactly are you up to here?
The motivation for this blog was a secure code review a few years ago, when looking at a client's email token generationI don't actually work as an RNN jockey for work- I'm a security consultant. . Frankly, I don't remember what their code looked like at all, but it probably looked something like this:
"""gotta make a token and send it to the client!"""
very_random_number = get_random_number()
two_factor_token = convert_representation(very_random_number)
send_email("Your two factor authentication token is:"
+two_factor_token,user_email)
save_token_to_user(user_id,two_factor_token)
Code like this undergirds the security of much of the internet. A user wants to reset their password, so they enter their email. We generate a secret code and send it to their email; opening the link in the email proves that the requestor is legitimate. Sometimes we text codes like this to users when they try to login to their banks; this type of association between a random number and a user is also the backbone of a huge chunk of cookie-based authentication.
Is this code secure? Well, it depends. Naturally, we might attack the email component (as emails are sometimes sent unencrypted, whoops) or we might attack the association between the data (maybe the token and the email are derived from attacker controlled data or whatever). The quality of the random number generation here matters as well, at least in theory: some random number generators are predictable, while others are provably difficult to attack. If we could predict this, it would be super bad- we'd just trigger the email to the victim, somehow predict the RNG, and be on our way. On the other hand, even if we are able to 'predict' this, we are still in trouble: there is no obvious way to go about it without prior knowledge of what convert_representation is up to.
I think machine learning provides the bridge here. The thought has hung in my mind for a few years, in fact; I've picked the brains of everyone I know remotely related to the field, and I've even hired some people to take a crack at it. So far, I haven't seen any prior literature suggesting that it's been possible or done, and nobody was really sure how to approach it. Finally, thanks to a generous grant from the Phil Brass Weird Ideas FoundationAKA DirectDefense who was happy to sponsor this research while I was not busy bug hunting for them! I was able to take a few weeks to think about it methodically.
The rest of this blog is structured in a pretty straightforward way: I talk about how numbers are generated at random in a computer, then talk about how to transform that notion of randomness into a learnable problemA basic knowledge of machine learning, and especially gradient descent will be helpful for understanding some of my thought process through this blog. . Not surprisingly, I will then solve that problem, and propose a roadmap for how to continue chipping away at the distance between my current progress and a usable attack.
Our Constant State of Sin
Computers, these fucked up little rocks we have forced to think, are gambling creatures. Despite the rigid constraints that we have imposed on them, we sometimes instead demand them to be fickle beyond our own capabilities, to choose a number more wildly than any human dare dream. For example, by invoking Xorshift128, a rather stylishly named fellow, you can choose a number between zero and about four billion (2**32, to be precise), which is a number that, while you do not often have a reason to choose at random, is at least a number whose neighbors you encounter at least occasionally. More excitingly, you can invoke this function a staggering 2**128 timesMore or less the number of atoms in every living person on earth. before you encounter a repetition in its pattern of randomness.
But how? I hear you cry. That is to say, A particular problem arises here, the one I think Von Neumann was referring to above: programming a computer is the art of telling it exactly what you want it to do, more or less in advance, and telling it exactly what random stuff to come up with, in advance, both defeats the purpose of the program in the first place and also poses fascinating logical challenges at the programming level. Certainly you do not have time to roll four billion of anything, and even if you did, writing each of those numbers down in some way would be a miserable use of time and hard disk space. On the other hand, cycling through just a few of the available numbers also sounds wrong; if you cycle through just a few hundred of the integers between 0 and 2**32, you're not really providing a lot of randomness.
We will set aside the question of what randomness really is and think about it from a programming perspective. We can define a Random Number Generator (RNG) as something that outputs a sequence of numbers. In order to make sure that they are as random as possible, we're also going to introduce something new: state. The state gets passed into this RNG function, and in addition to outputting a random-ish number, it is going to output new state- this state will be as big or bigger (usually much bigger) than the output. Then we're just going to feed this output state back into the RNG to generate the next number in the sequence- and that's going to give us new state, which will let us continue this for quite a while. One point of confusion is that sometimes the output is also used as the stateAstute readers will wonder: where does the original state come from? Fascinatingly, movement of the mouse, entries into the keyboard, and other minutiae of computer operation are used to generate a very small amount of randomness- that is, at some level the start comes from the simple uncertainty of everyday computer use. There isn't a lot of randomness available here, so the RNG serves to stretch it out over a longer period of time. .
To take this into the concrete, we will consider an RNG, the Middle-square method. Relatively ancient by RNG standards, it was invented by Von Neumann sometime in the 1940s, when he was busy inventing almost everything else. A number of N digits is squared, and the N/2 middle digits of the result are taken both as the output as well as the state to square for the next iteration. The simplest case, n=2, works as follows: we start with 43, square it to produce 1849, and then take the middle two digits to get our result, 84. This 84 is also our new state, so next time we're fiending for the results of a d100, we square it again, 7056, taking the middle to get 5, our output and our new state. Okay, so next is 25, which we'll call 0025, which gives us 2, which gives us 0004, translated as 0...
Uh oh. We seem to have run into a dead end here. 0 squared is of course 0. These numbers are not looking so random anymore. In fact, the behavior is pretty bad no matter what number you begin with. The figure below lists all the states/outputs showing that the tendency to degrade towards cycles is pretty unavoidable.
Performance for the version with 4 digits of state is better; the average length of time before being trapped in a cycle is after 43 outputsAnother useful property of these RNGs is that it is pretty obvious when they are starting to break down- among the 10000 numbers the 4-digit version can output, only 0, 9600, 1600, 5600, 8100, 100, 4100, 2916, 2500, 3009, 5030, 3600, 7600, 3792, 2100, 6100, 540 immediately lead to decay. . That code looks something like this, just so you get the idea:
def von_neumann_generator(state):
"""The version with a 4 digit state/output
not to be confused with the one above, that
has two."""
#e.g. 1234**2->1522756
square = state**2
#1522756 -> 01522756
formattedSquare = "%08d" % square
#01522756 -> 5227
next_state = output = int(formattedSquare[2:6])
return (next_state,output)
state = 1234
for i in range(20):
state,output = von_neumann_generator(state)
print(output)
You can see in the above example that the state and the output are identical, but there is no particular reason this has to be the case. For example, we could have the state be the inner four numbers, with the output being the outer four numbers:
def much_better_von_neumann_generator(state):
square = state**2 # e.g. 1234**2->1522756
formattedSquare = "%08d"%square
output = int(formattedSquare[0:2]+formattedSquare[6:])
next_state = int(formattedSquare[2:6])
return (next_state,output)
state = 1234
for i in range(40):
state,output = much_better_von_neumann_generator(state)
print(output)
This RNG is also not quite ready for prime time, but the relationship between the output and state is already harder to guess. However, they are clearly interconnected in some causal sense, a fact we will return to in a bit. For now, we are starting to see a few important tensions in the design of RNGs already:
- Unpredictability – Increasing the number of digits in the output/state increases the unpredictability of the output. Sometimes less adroitly designed algorithms (like the one above) will eventually degenerate to some kind of undesirable low-randomness state, but most ones in use in computers simply will iterate through their entire state in some order before returning to the original one. Among the generators that look superficially okay, there are a lot of mathematically interesting ways to verify this intuition: we can count the number of bits to make sure it is evenly distributed; we can figure out if the runs of ones and zeros look OK, and a horde of other more complex criteria. On the far end of this difficulty spectrum lies the Cryptographically Secure Pseudo Random Number Generators (CSPRNGS), where someone has gone through the trouble of proving that predicting the subsequent bits is virtually impossibleBut not necessarily completely impossible. Predicting these bits (or more precisely, discerning the output from true random noise) is in NP, a class of problems in computer science which are thought to be generally computationally infeasible. Because neural networks are well-understood to be capable of approximating some NP functions, it is actually not clear to me if there is an a priori reason to believe a NN could never learn to predict one. . So then, why don't we always just use CSPRNGs? Well..
- Performance – Unfortunately, CSPRNGs are pretty slow. Opportunities for high-performance RNGs are actually more common than you might imagine: almost every web site is constantly vomiting a stream of random numbers to users who are visiting or logging in, and in online games they are virtually ubiquitous. At the low end of things, embedded devices (like your bitcoin-mining toaster, or IoT-connected trash can) may need to more frugally use their available CPU cycles and so are not willing to sacrifice precious cycles just for needless cryptographic guarantees. Or maybe you are writing Doom in 1993 and you just need the fastest thing that looks kinda random, so you just scramble the numbers from 0 to 255 and hard-code them in a table. So just using a CSPRNG for everything isn't necessarily rightAnd frankly, they are kind of a pain in the ass to implement, so by the time your language has blown up in popularity you already implemented
randomwith a Mersenne Twister and everyone is yelling at you. . That being said, the high-performant algorithms in use these days are much better than the one I demoed above. - Political – Okay, so this doesn't really fit with the other two in an easy way but it has to be mentioned. Sometimes the NSA comes out of the black obelisk or whatever and tells you that certain changes to your RNG have to be made. Sometimes they release a standard for a new Very Secure Ultra Good RNG and it's backdoored. Sometimes your government tries to ban exporting the very concept of secure code to anyone and so everyone else has to use bad crypto until you can get your friend drunk enough to get a Perl tattoo of RSA's encryption algorithm the night before his flight to Amsterdam. Sometimes your coworker printed out an article about how Mersenne Twisters are vile beyond God's redemption, and so using one will get you fired from your job at the stochastic matrix factoryhttps://arxiv.org/pdf/1910.06437.pdf . Cryptography is just a very weird field in some ways and so there are lots of other reasons that people have very intense feelings about it.
This has led to an exciting and dynamic variety of RNGs that are constructed from a few general primitives. You need operations that you can apply repeatedly to cycle through a very fixed list of outputs, which means most of the operations we use on a daily basis don't really suffice. Bitwise operations (converting two numbers to their binary representation and shifting or otherwise transforming them) are combined with modular arithmetic and a cursory knowledge of group theory to robustly create numbers that look indistinguishable from noise at first glance. Quick, what do 3701687786,458299110,2500872618, and 3633119408 have in common? They are the first four outputs from my implementation of Xorshift128, and as far as I know, that is more or less their only interesting relationship. Even without the rigorous mathematical guarantees of their more cryptographically secure brethren, they and their two million nearest neighbors in the sequence are alien to me, as predictable as the roll of the waves of the ocean.
It doesn't mean that doing so is impossible, however, it is just hard. These functions are generally reversible in the mathematical sense, and their crunchy bitwise nature has made them the target of SAT solver-wielding lunaticsMy personal favorite of these is definitely the guy who bopped an online casino in real time. . However, for most real-world applications, predictability is also made more or less infeasible by a few interrelated factors:
- Encoding – RNGs are consumed by a variety of different sources, and all of them have a variety of decisions about encoding: some are making 6 digit two-factor authentication tokens, some are doing 2d6 sword damage, some are outputting 32 character hexadecimal session tokens. Also, the nature of this encoding is not necessarily clear in the case of a closed source application. We also don't know how the excess entropy for a specific random number is being used: the invoking API may simply truncate the top 29 bits of randomness to roll 1d8, or it may slyly apportion the output into fixed 8 bit slices to improve performance by reducing calls, or something else.
- Transformations – Another problem is that other entropy preserving transformations are possible. Bit order may just be straight up reversed for some reason, or maybe the developer decided to XOR the output with "TIMROX" or whatever. Or maybe it's just multiplied by 2 because that's how much damage the laser pistol does.
- Continuity– The above both assume that you get perfect vision into the output of the algorithm, which is uncommon because normally an application's randomized output is being consumed by different mutually exclusive groups of users. You never see another user's session or 2fa token; you never see the random damage from another warrior wandering the lonely hills of the sea witch or whatever. This one is especially challenging because you also don't really know how much of the output you are missing; there is no clue as to how many steps forward the state has shuffled.
These underlying problems are very important, but they are not essential to what I believe is the hardest part of the problem, which is getting a neural network to learn any of this in the first place. So I decided to start there: the above-mentioned Xorshift128 has 128 bits of state and 32 bits out output. But without looking at the state, how do we attack this problem?
The Math Part
After thinking about the above problems for a while, they eventually congealed into my brain into something useful. There is some function F: statet-1->(statet,outputt). But this means that the state is deterministic from the previous state, so we can apply this as many times as we want. For example:F: statet-4->(outputt-3,outputt-2,outputt-1,outputt,statet).There are two interesting things to observe here:
- There is good reason to believe that each state that can be output by this function lines up with exactly one set of 4 outputs. It's clear that there is not a one-to-one relationship between output and state, because the output is 32 bits for a given step, and the state is 128 bits. So the minimum number of outputs we need is 4, if we want to be able to uniquely map these. Do we need more than that? Probably not, if the RNG is well designedIt's clear that there are RNGs where you do need more state. My brother provided JOSHRNG, where
OUTPUT= state%10==0?state:0;state++. Even if the state and the output are the same size here, you don't always get useful output. Probably the entropy of the output sequence is related here. The fact that my intutition worked for this problem (which indeed seems to be able to more or less perfectly learn with only 4 previous outputs) may not be useful for other problems in the family though. . - If you are willing to entertain my wild notions that the state and the sequence of outputs are uniquely linked, you don't really need to think about the state at all. That is, if you're willing to believe that the next 4 32-bit outputs of
Xorshift128are uniquely mapped to a given 128 bit state, then you don't really need to think about the state at all. Each unique sequence of 4 numbers only appears once through the entire2**128bit state, and so if you have them and can predict that state, you can easily predict the next number.
After the above pondering, I wondered how easy it was to train a neural networkWe've arrived at the machine learning part of the show. If you wanted to brush up before diving in, now would be the time! to learn the above function. That is, the obtuse F:(outputt-4,outputt-3,outputt-2,outputt-1)->(outputt), which predicts the output of Xorshift128 given only the previous four outputs. It almost certainly exists, and there are some aspects of the problem that make it pretty appealing from an ML perspective:
- Lots of data – I can generate two trillion training examples relatively easily. And there's no noise in the data. Unlike image detection where the same cat can be photographed from a variety of angles in anywhere from bright sunlight to darkness, all the data is pristine and beautiful.
- Even data distribution – All of the data is relatively evenly distributed over the problem space, as well. This means that overfitting is relatively unlikelyOR IS IT?!?!?! because the inputs and outputs have a singular, complex relationship.
- Model design is simple – There are some complex and unpredictable bit juggles which can happen between almost any two bits. These sound like dense layers to me. There's also some kind of hidden state which we want to learn over the sequence, which maps pretty well to an LSTM. So we don't need any fundamental breakthroughs in model design, at least at first glance.
I am going to change this data around a little. We will convert each 32 bit output of Xorshift128 to its binary representation: each number will be converted to a 32-bit list of, well, its bits. I know that this is the underlying representation used by almost all RNG code, so it feels like a natural choice. Additionally, each training case is (theoretically?) independent from everything other than the previous 4 numbers, so we'll slice our list of every single output into individual strides of that data: 1,2,3,4,5,6,7,8,9 becomes [[1,2,3,4],[5]],([2,3,4,5],[6]). Then, each of those individual numbers is converted to binary. That looks like the below, though I'll convert them to 4 bit numbers in this example so it's more manageable to read. Just pretend all of these lists have a lot more zeros:
x1 = [[0,0,0,1],[0,0,1,0],[0,0,1,1],[0,1,0,0]] #[1,2,3,4]
y1 = [0,1,0,1] #5
x2 = [[0,0,1,0],[0,0,1,1],[0,1,0,0],[0,1,0,1]] #[2,3,4,5]
y2 = [0,1,1,0] #6
And so on. In machine learning terms, we would like to take this sequence of length N and slice it into some tensors: a 32x4 input tensor and a 32x1 output tensor. All that is standing between us and the finish line is writing some performant numpy code that performs reshaping on multidimensional tensors. Yes, nothing could go wrong thereThe resultant code in the script i will publish below relies on the aptly named stride_tricks module of numpy. Some free advice for you in your future programming career: if you are considering the use of a library function with tricks in the name, your life may be leading you to a place that you don't really want to go. .
So the starting network is simple enough: An LSTM to capture state based dependency, a few dense networks to cover the endless shuffling, then an easy finish with a 32 bit final layer. Early experimentation more or less resembles this:
model.add(LSTM(units=1024,activation='relu',input_shape=(4,32,),return_sequences=False,))
for depth in range(5):
model.add(Dense(512,activation='relu'))
model.add(Dense(32))
Our success is relatively easy to measure, as well- we'll just count the number of correct bits in the output. And if we fail, well, we can just add more network layers or network width until everything works out! All that's standing between me and success is melting my beleaguered laptop's GPU.
Unfortunately, one small problem with the above approach is that it did not work. Many opportunities for failure were covered in my machine learning 'educationCoursera, DeepAI, screaming at the Keras documentation, cursing the god who brought me into this world, etc. ': Network overfitting, the network learning a little bit and then giving up, vanishing gradient problems from the intricacies of network design. But in this case, several hundred steps with the default gradient descent learned nothing; it stubbornly stuck to 50% accuracyWhich may sound good, but it is the expected accuracy from guessing. no matter how many layers or how much data I added to the model. I decided to go back and question my previous assumptions: What actually made this problem difficult for neural networks?
One nasty reality is that, in some sense, the function is not smooth- small perturbations in the input result in very drastic changes in the output. For example, in image classification, a picture of a bear that has one pixel blacked out is, in some sense, still a picture of a bear- similarly, two pictures of a bear taken seconds apart from slightly different angles are both more or less pictures of a bear. On the other hand, a change in bits of output from an RNG suggests that the underlying state is different, which will have cascading effects on subsequent callsSpecifically, the avalanche property is something RNGs try to aim for – we would like single bits of state being different to change half of the bits of the resulting output if we are making random numbers, because that's what you would expect from, well, random chance. . This is a result of the XOR function's relative difficulty in modeling as a smoothly differentiable function. So in my mind, the solution space is very 'spiky'.
Another problem is the predictor has to work super hard. There are 32 outputs for each test case, and they are all (again, in theory) perfectly uncorrelated with one another. Similarly, each input consists of broadly uncorrelated bits- no two or three of them exhibit any obvious, discernable pattern. So both the input and output data have no simple relationships, no obvious subproblems to solve that can lead the network in the right direction. Or, to put it less mathematically, this output is difficult to predict because it's designed to be as unpredictable as possible. Oops!
The upsetting thing about these intuitions, to me, is the difficulty in verifying them. This network has about six million parameters, which output some kind of function f. We can measure this function f in terms of its accuracy on the training set; thus, we can also think of all of the six million parameters as a six million dimensional space that outputs some number between 0 (for a function that somehow deliberately fucks everything up) and 1 (for one that predicts everything perfectly)This is a map between the big list of parameters for the different neurons in the network and the output. That is, all the parameters [p1,p2...p6,000,000] generate a function f, and the average performance of that function on the training set is between 0 and 1. I'm sure it's pretty easy to have a network learn to output only bits between 0 and 1; so most of the models expressed by this dimensional space are going to be very close to .5. Sadly, I have no easy way to model this enormous, messy space in a way that shows the entire thing; no chance with my pathetic mortal brain of visualizing it like I would an ordinary problem.
Having failed in my original task, I decided to step back and think about what problems I might have in this noisy, monstrous mess of a space. Clearly the data was spiky, but at what scale? I have no idea how densely the valid solutions to this problem are packed in space, nor any idea how to find them. So I wondered if the learning rate–the speed at which the network roamed through this space. – could be big enough to skip over it entirely. There was also no automatic guarantee that having a larger network was better- adding more parameters made the remaining ones more sparsely filled. But too small didn't seem great either- if the network was learning, perhaps it was far, far too small to make sense of the problem space.
In the end, experimentation seemed like the only way forward. First with brute-force and then the aptly named keras_tuner, I began to search my way through the problem's hyperparameters – the speed at which it learned, the complexity of the network, and so on. Most of these experiments were, of course, fruitless, but I got some good stuff too:
- Learning rate is everything – I looked through learning rates as small as 10**-12 (resulting in constant, sad numeric underflow crashes) and as large as 1. In this case the right answer was about
10**-3, but there is no a priori I can see why any parameter is better or worse for a certain RNG. - Extremely simple networks work – The end network is 1 LSTM and 5 Dense Keras layers, followed by an output layer the size of the RNG output (32 bits). The small problem space (only 2**128 possible outputs) is a possible factor here, or the underlying mathematical simplicity of the transformation. The entire thing trains on my Geforce RTX 2060 in a few hours, even thought it is the GPU equivalent of a Toyota Corolla.
- Overfitting is still a problem – Perhaps you spotted this naivety earlier; I only trained the network on 200,000 inputs, reasoning that overfitting was better than no fitting at all. In retrospect, very incorrect to assume that it was impossible for overfitting to occur on any problem.
Still, after an exhaustive search of the hyperparameters, I was making progress- I upgraded to 600,000 training samples and chose the brute-forced parameters. ~80% training, ~60% test. Still a stubborn gap, but the solution was simple, right? Just add more data. Changing a single line of code shoved in 2 million examples, which seemed fine.
Sadly, for the second time, things were not fine. In contrast to every other machine learning problem I know of, where adding more training data makes things work better, adding more data here made things work worse. In fact, the model was unable to learn anything with 2,000,000 training examples. Worse still, it learned nothing slowly, meaning I was spending agonizing hours watching the epochs tick by with nothing to show for it.
Why is learning so poor? I decided to speculate wildly. One weakness in this model design is that it is somewhat large compared to the size of the data- 6,000,000 or so parameters compared to only 2,000,000 pieces of training data. In particular, the first LSTM layer is also quite wide compared to the size of the problemMy idea for this unusually large layer was that there was clearly a lot of state to remember between steps, and having all of that state perfectly preserved was nice. For the same reason that changing some of the output greatly changes the subsequently expected output, small noise in the state of the RNG seems like it will fuck everything up here. . Maybe the gradients are very evenly dispersed across different nodes, and averaging them out from many different inputs makes them cancel out.
So, overfitting on the training set is obviously not desirable, but nor is not fitting at all. My thought in the end was some kind of model tempering: I'd start by running the model against a smaller version of the training set even though it overfits. Getting near the correct function in the 'parameter space' seemed to be quite a challenge for the larger model, and overfitting certainly works here. Once I have an overfit, but kinda working model, I will train it on the entire training dataset for a few epochs. The hope here is that although the model will suddenly have to generalize, causing lots of movement in the parameter space, the fact that it is somewhere in the right neighborhood makes those jumps more likely to be somewhere that is useful for the whole data set. After all, even if the function is overfitting, in some sense the smaller training set is equally distributed through the input space, and so all of the unlearned examples are pretty close. If this works, there's no reason to not do it a few more times- every iteration should bring us closer and closer to the correct f. I am keenly interested if enough cycles with the full set T will cause catastrophic interference- it did not in the limited epochs I ran the data through, though.
Anyway, I think the results speak for themselves:
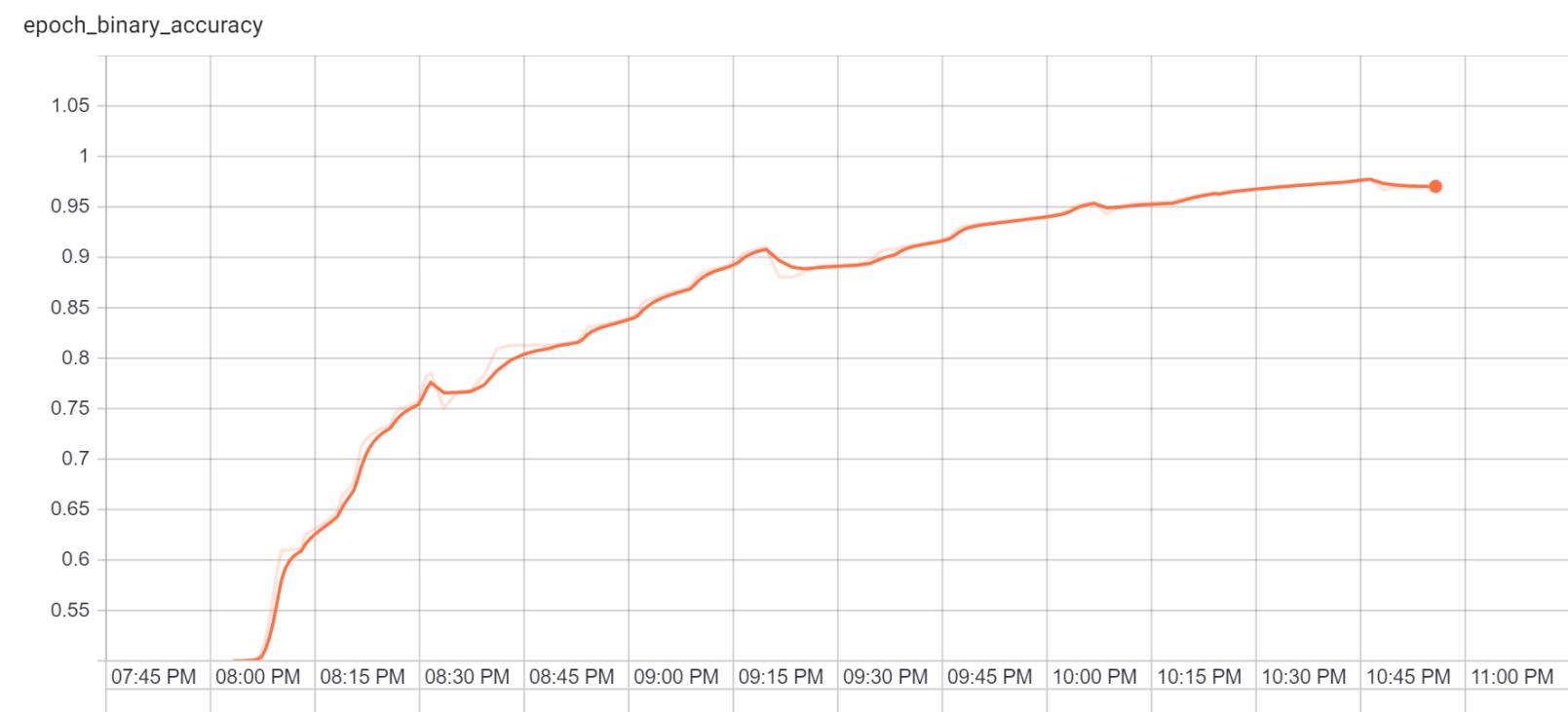
This model actually took a few times to succeed- previous runs were peaking anywhere between 75% and 80%, with the tempering effect eventually unable to make any progress (but never hurting things, either). Clearly these are local minima, but why exactly this run escaped or to what extent better performance is possible is not yet clear to me.Shrewd tensorflow enthusiasts will note that this is in wall time instead of measuring performance by epoch. It turns out that Tensorboard gets very sad when you try to restart training epochs on the same model, something you will probably notice if you try to run this code. Still, just to make sure I wasn't losing my mind, I verified it against 2 million separate examples that it had never seen before and still saw the same robust performance.
This is a way to get to the correct function, but I suspect it wasn't the best way. There are other promising lines of thought which I'd like to experiment with, including:
- Cosine activation function– Normal activation functions, which I didn't really touch on here, are specially constructed to avoid real analysis problems. My first thought was that cosine was an appealing function for some of the intermediate activations for some interesting reasons: addition of incoming weights naturally approximated the XOR function, the input/output was bounded by -1,1. In the end it didn't really work so well, but some kind of opportunity for the network to flow through gates that use this function is one I'm looking for in the future.
- Smaller learning rate – I spent some time trying to tweak the learning rate for the larger training set in order to get the model to learn, and the problem is (at least in my testing) relatively sensitive to this rate. Does a different learning rate affect the performance on a large number of examples? It's an important question, even if it's unlikely to beat the current performance of training on such a small number for most epochs. Naturally decreasing the learning rate over time might work too.
- Model simplification – I started out with a pretty large model relative to the training size, which seemed to (in the end) successfully create the right network for the job. Model depths close to this size seem to be OK, but I didn't do a lot of tests on the widths of different networks.
I'm not aware of any other information or research about the model 'tempering' technique I described above; I haven't even tested the hypothesis above that it is linked to the data being well-distributed in the space It resembles data pre-training of course, but normally you don't pre-train on the same data set. . This is actually the first time I have built any type of novel model, which naturally suggests that this problem has already been tackled before and that this technique was already known. So rather than continue chipping away at it with increasingly feral code, it seemed appropriate to release it for everyone else to take a look. Here is the code if you are into that.
Onward!
I've made good progress on the problem that spurred this research; I think that predicting the sequence at all is the hardest thing to do But I don't have high confidence in this guess. The cost of intuition taking me from place to place is that sometimes intuition leads you down a dark alleyway and leaves you in a dumpster with no kidneys. . The road from here to practical attacks has a few important problems, some of which I've touched on before:
- Generalization – How applicable is this architecture to other RNGs in the search space? I think there is good reason to believe that this will generalize to other RNGs in the same family-
Xorshift128+, this research project's original target, differs only in the number and size of its shifts and xors. So there are no new types of functions to learn here. On the other hand, the Mersenne Twister is rocking2**219937−1bits of state, so there is a good opportunity to see how much this approach scales. - Transformation – Most web applications rely on a fixed RNG provided by the platform or the target language. There is no particular reason to believe that I couldn't train a specific model for each platform's RNG. We'll still need to learn the correct transformation of the data from RNG output to rendering in the web app, but with Transfer Learning we can use the RNG network and just add a few layers to learn the transformation as well. The underlying learning problem is probably much simpler here: for example, each bit of the base64 encoding of some random output is probably only correlated with a few adjacent bits from its input, an architecture well-suited to a convolutional network. We see learning on complex image tasks here with thousands of training data (rather than millions) when transfer learning is used. It seems reasonable to guess that we can hope for good speedups like this on a problem where the data being dealt with is much smaller.
- Harder transformations – What if some of the data is just thrown out? Like, maybe your 2fa token is just
RNG_Output%10000. My intuition is that this just stretches the amount of data that's required out- if we only get 16 bits of output from the RNG, we just need twice as many outputs. I will probably be testing this right as you're reading this! - Missing data – Another obvious problem: what if we just get small chunks of the data, rather than all of it? In some sense, we are still getting decent data here if we're only missing one out of ten or one out of twenty cookies/2fa tokens/etc- 90% of the slices will still be correct. This will introduce noise into the final network, which is not desirable (especially on a problem that is seemingly so sensitive to noise.) On the other hand, there is clearly some structure to be learned here: if you are guessing how many tokens you have skipped over, ten is more likely than two billion, which is more likely than 10**20, which is still barely scratching the surface of the state of the RNG. This is clearly the hardest remaining problem.
The interesting thing about both of the latter problems is that they require a certain discipline in the network's learning - the less training data you require here, the more likely it is you can get a string of uninterrupted sequences. This means that the surrounding architecture has to be as simple as possible. My first thought here is that some kind of invertible function would be nice to learn. If we can somehow define the transformation to and from, say, base64, with the same parameters, we halve the number of necessary ones and greatly reduce training complexity.
What do I take away from this?
The reaction I got from most of the people I showed this research to was "Wait, what?". Artificial intelligence in security has struggled thus far to catch on for the offensive side of things; countless data panopticons are excitedly hoovering up IDS data and doing their best to make it impossible to breach networks in the first place. As the ML research equivalent of a feral dog, I have no ability to work on these problems; I just don't have enough data or computing power. On the other hand, this problem excites me because it's so completely different: the data is easily available, and the network is simple enough to train on my gaming laptop in a few hours, and the underlying innovations can come from different designs. There is good reason to believe this will be true for most practical attacks as well, since we have to very greatly constrain the amount of learning for the problem in order to get practical attacks from only a few thousand tokens.
So I would take that away as the first lesson- attacking this problem isn't as hard as it seems. None of this is. I've never even built a network from scratch before, meaning it's pretty simple for a beginner to attackA very sobering thought is that there are... 👁️organizations👁️ with much more computing power and manpower than I have to work on these problems and a much more robust understanding of the underlying cryptography. Haunting! . There's not even any guarantee that the foundations I've laid here are the best way to approach the problem, but they do work.
The second lesson is much simpler- it's probably time to start upgrading to more secure random number generators. It's not clear to me that CSPRNGs are invulnerable to this problem, but it's certainly easier to believe they will be harder to get throughOn the other hand, if CSPRNGs are not invulnerable to these techniques, the internet will become a much more exciting place to live! . Additionally, there were already plenty of good reasons to start limiting 2fa token output per hour, but hopefully this article has provided several extra ones.
If you have any questions or comments about this article, please feel free to email me at john@airza.net.
Acknowledgements
To Phil Brass, for seeing the underlying value of this research, and to our mutual patron, Direct Defense, for being willing to sponsor it. Naturally, I highly recommend them for your computer security based needs ;)
To Joseph T, who I worked with on a much earlier incarnation of this model that didn't work, but helped me understand how to implement my own version.
To everyone who was willing to review this long-ass article.
Special thanks to Tsukimi, who was a constant companion in my 4 AM debugging... once she figured out how warm the GPU fan was.
 Moral support.
Moral support.
But Wait!
I am currently looking for both short-term and long-term work. If you're looking for someone who is good at things, have a look to see what I am good at: computer programming, writing, Magic, etc. Or if you had something else in mind, send me an email and let's see what we can do.